너무 공부하기 싫어서 미루고 미뤘던 일상의 패턴을 다시 잡고자 메타코드를 들어갔다.
이전에 무료강의여서 신청해둔 선형대수학 기초 총정리 강의를 먼저 켰다.
딥러닝에 활용되는 수학을 정리해둔 강의라길래 듣고 오늘의 포스팅을 작성하려 한다!
0. 강의 소개
서울대 박사과정을 밟고 계신 강사분이 딥러닝 기초를 위한 개념 강의이다.
아래의 링크를 눌러 메타코드 사이트에서 로그인을 해주고 강의 영상 카테고리 > 무료강의에서 바로 신청하면 된다.
조만간 유료로 전환될 예정이라니까 빨리 고민하지 말고 수강신청 하자!
메타코드M
빅데이터 , AI 강의 플랫폼 & IT 현직자 모임 플랫폼ㅣ메타코드 커뮤니티 일원이 되시기 바랍니다.
mcode.co.kr

1. 강의 내용
선형대 수학을 간단하게 요약해보겠다.

먼저 기본적으로 스칼라, 벡터, 행렬에 대해 표시방법부터 알려주신다.
표시방법은 정수, 자연수, 유리수, 실수 를 각각 수학적으로 어떻게 표시하는지부터 설명해주셨다.
그리고 간단하게 행렬에 대해 설명해주셨는데, 행렬은 2차원 배열에서 세로 X 가로 형식으로 나타내며 벡터의 나열이라고 설명해주셨다.
강의가 전반적으로 행렬을 중점으로 진행되었기에, 고등학교때 행렬을 배우지 않아서 공업수학으로 잠깐 배운게 다였던 나는 행렬이 항상 헷갈렸어서 이번 기회에 행렬에 대해 다시 잡고 갈 수 있는 시간이라 너무 좋았다.

이 부분은 사진만으로 본다면 중간에 오타도 있어서 무슨말인지 헷갈리고 이해가 안될수 있다.
내가 이해한 걸 기반으로 쉽게 이해할 수 있도록 설명을 덧붙이자면,
먼저 실수의 가로 세로가 모두 3인 행렬이 존재하고, 이 행렬을 A로 가정해둔 상태다.
행렬은 세로 한줄씩을 차원으로 보는데 화면의 예제에서는 1 0 1 이 a1 / 0 1 0 이 a2 / -1 0 -1 이 a3 차원이다.
행렬은 세로의 크기가 같아야 연산이 가능하고, 연산을 할 때 크기가 작은 행렬(벡터)로 나타나게 된다.
그래서 예제에서 보이는 c1, c2, c3가 하나의 벡터, 행렬로 곱셈을 하게되는 것이며 왜 그렇게 되는지에 대해서는 좌측 하단의 식을 참고하면 이해가 될 것이다.

내가 추후 참고할때 헷갈릴까, 이 글을 보고 무슨말인지 헷갈리는 분이 있을까하고 아래에 식이 추가된 설명을 가져와봤다.
a1, a2, a3 는 모두 A에 속한다.
그리고 이것을 다르게 표현하자면 a1은 A11 / a2는 A12 / a3는 A13으로 표현한다.
그 이유를 설명하자면, (3, 4, 5) 라는 행렬 결과에서 3은 첫번째(x축)에 해당한다.
그렇기에 첫번째 값이라는 의미에서 b1이라고 두었을 때, b1에 해당하는 공식을 사용하면,
3X3 행렬에서 A에서의 각 세로 개체들을 묶어서 순서대로 본다면 a1은 첫번째, a2는 두번째, a3은 세번째 순서에 해당되기에 위의 공식으로 표현된다.
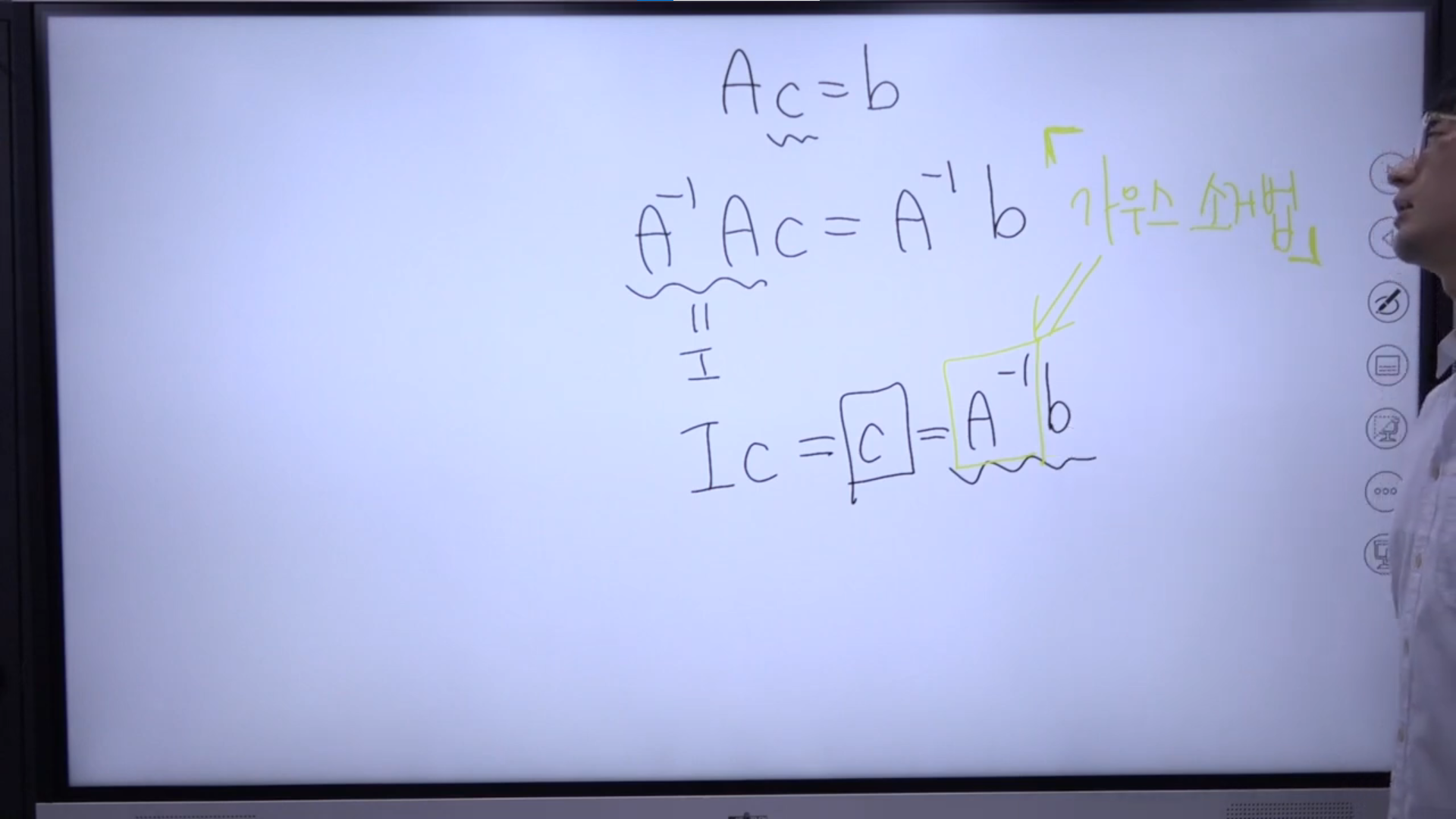
Ac = b 일때, c를 구하고 싶으면 A의 역행렬을 곱해서 구하면 된다고 한다.
역행렬과 행렬을 곱한값은 단위 행렬이 되기 때문인데, 이 단위행렬이 곱해진 c값과 c는 결국 같은 것을 의미한다.
단위행렬이 무슨 의미인지 잘 모르겠어서 gpt에 검색을 해봤더니 이 말이 이해가 됐다.
설명을 들을때는 Ic가 c의 배수 이런것을 의미하는줄 알았는데, 단위행렬은 주 대각선상의 값이 모두 1이고 나머지는 0으로 채워진 행렬이라는 설명을 보곤 기억이 났다.
이 강의에서 행렬의 계산법을 가르쳐준것은 아니기에, 이 부분을 따로 찾아보고 이해하게 되었다.
행렬에 대해 잘 모르거나 이해하기 힘든사람은 나처럼 gpt 에 예시를 들어달라하고 보면 금방 이해가 갈것이다!

난 이 부분은 수강하면서도 이해하기가 어려워서 일단 듣기만 했는데, 바로 뒷부분에서 풀어서 설명을 해주셨다.
행렬이 3개가 존재할 때, 두개의 행렬이 서로 종속일 경우 결국에 3개의 행렬이 만들어 내는 것은 부피가 아니라 넓이가 되어버린다.
결국 부피를 구할 수 없게되고 이에 따라 역행렬이 존재할 수 없게된다.
그러면서 위의 조건들이 다 엮여서 참이되는 구조가 된다고 한다.
그래도 이 부분은 이해하기가 어려운것 같다..ㅋㅋㅋ

맨 처음 행렬에 들어갈 수 있는 부분은 같이 곱해지는 벡터에 길이를 팽창하거나 수축하는 수이거나
원점중심으로 컴퍼스로 원을 그리듯이 회전하는 것이 가능하다고 설명해주셨다.
사진을 참고해서 설명들은 것을 글로 옮겨보자면, [1 2] 라는 벡터가 있고, 그 벡터는 노란 형광펜을 중점으로 배수가 될 수 있고 반대방향으로 전환될 수도 있다.
그리고 길이는 고정된 상태에서 회전해서 움직이는 두가지 중에 하나에 해당되는 것 같다.

2차원 행렬의 회전에 대해 더 알아보는 시간을 가지면, [1 2] 라는 벡터가 있을 때, 같은 길이의 X'과 Y'을 기준으로 회전에 적용해보자면,
X' 의 가로 길이는 X cos파이, 세로 길이는 Y sin파이 이며
Y' 의 가로 길이는 -X sin파이, 세로 길이는 Y cos파이 가 된다.
각각 수식으로 표현하면 위의 사진의 공식처럼 되며, 그 아래에는 이 식을 행렬로 변경해서 표현한 것이다.

결론적으로 행렬과 벡터의 곱을 하게되면 벡터의 크기에 따라 왜곡되는 다른 결과를 볼 수 있게 된다.
벡터의 크기(m)가 행렬의 차원수(n)와 동일한 경우에는 공간의 변형이 일어나게 되고, 그 공간에서 이어봤을 때, 그래프로 확인해보면 평행사변형의 모습을 띄게 된다.
벡터의 크기가 차원의 수보다 클경우 차원을 새로 생성할 수 있다. (강사분 설명이 이런걸 봐선 필기는 잘못 작성하신듯함.)
벡터의 크기가 차원의 수보다 작을경우에는 차원을 눌러서 정보를 압축하는 역할을 한다.

앞의 설명들은 행렬의 고유값과 고유벡터와 연관되어 있다고 한다.
어떤 행렬이 있고, 좌표 공간을 왜곡시키는데, 이 때 벡터들이 함께 존재한다.
여기서 벡터가 회전을 하지 않고 길이와 방향만 바뀌는 특정 벡터를 고유벡터라고 하며,
이 고유 벡터에 해당하는 길이의 배율은 고유값이라고 한다.
이 설명을 듣고 사진의 수식을 본다면 어느정도 이해가 갈 것인데, 그래도 어렵다면 강의를 직접 참고하길 바란다.
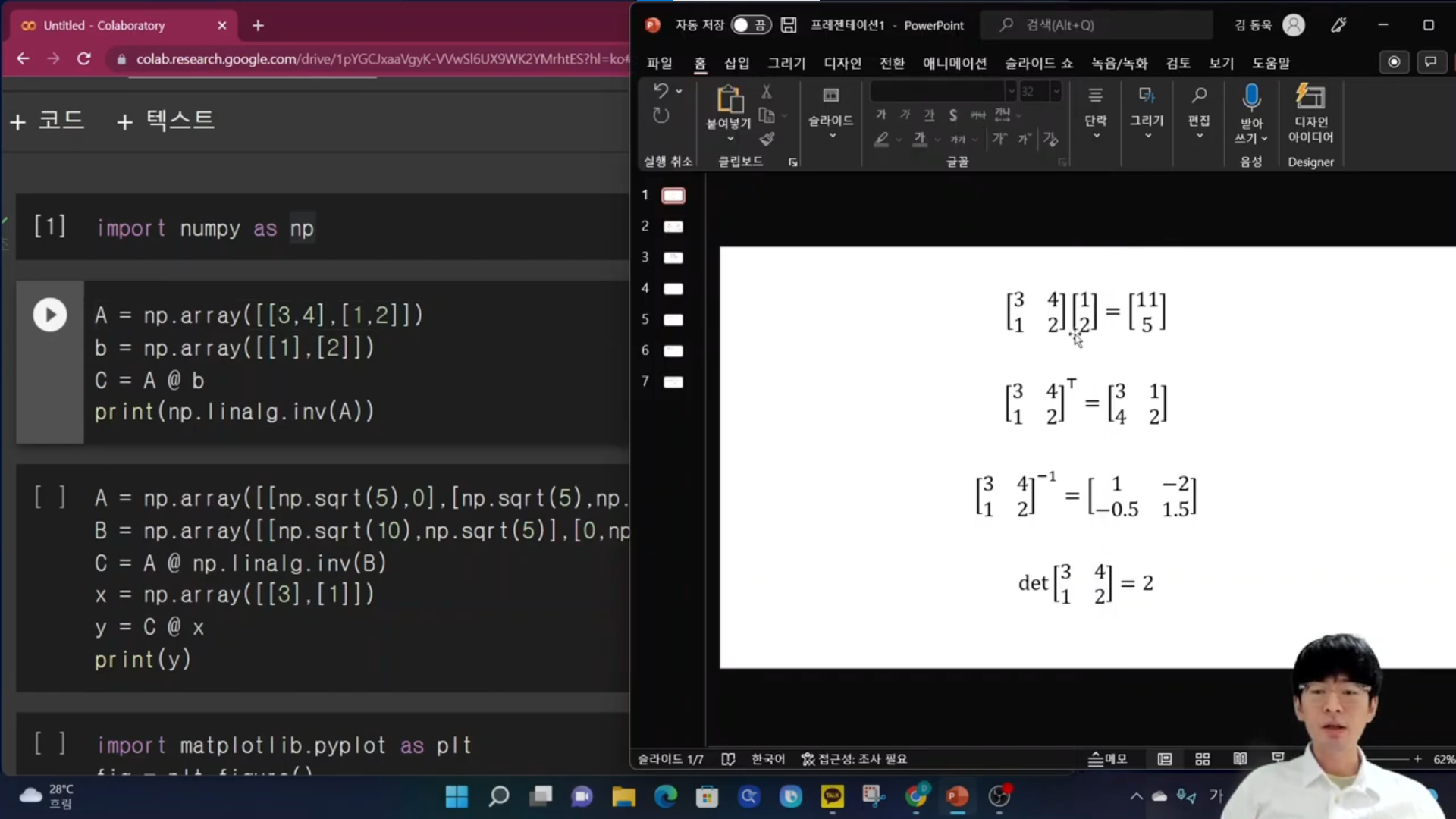
이 수업의 장점은 행렬에 집중된 개념만의 강의가 아니라 실습도 함께 제공하는 강의라는 점인것 같다.
무료강의에다가, 실습 파일로 파이썬 코드가 무료로 함께 제공되기에 혼자 실습해보라고 주는가보다 했었는데,
강사님께서 numpy 행렬을 사용하는 예시코드를 설명해주시면서 코랩기반으로 직접 보여주셔서 코드를 이해하는게 더 수월했다.
나는 이 실습파트를 로컬 주피터 노트북을 사용해서 함께 진행하고, 코드에 대해 이해하기 위해 GPT를 이용해서 주석으로 간단하게 해석을 달아두는 것으로 학습을 마무리했다.
2. 수강 후기
먼저 이 강의 중간중간 카메라가 잠깐씩 초점이 나가는 경우가 있었다.
길게 나가있는 것은 아니지만 집중하다가 중간에 집중력이 살짝 흐려지는 정도였어서 이 부분은 아쉬웠던것 같다.
이 강의의 내용은 행렬 파고들기라고 해도 무방할 정도로 행렬에 대해 알려주는 강의인 것 같다.
강사님은 쉽게 설명해주시지만, 행렬이 쉬운 파트가 아니다보니 이해가 안되는 부분이 중간중간 있긴하다.
이런 부분은 개인적으로 더 찾아보고 공부하는 것을 추천한다.
선형대수학을 수강한지 몇년됐다 보니, 대학시절에는 어떤 강의었는지 기억이 잘 안나지만 numpy를 활용해서 실습부분을 첨가해둔 내용이라 참고하기 좋은 것 같다.
그리고 오류인지? 현재 사이트에 2강 내용이 3강에 그대로 있다.
편집 실수가 일어난 것 같은데, 2강은 안듣고 3강으로 넘어가서 실습이랑 바로 연결할 수 있게 되는 것이 좋을 듯 하다.
코드 실습 시간도 조금 더 길고 자세했다면 더 좋았을 것 같지만, 무료강의로 제공되고 있는 지금 시점에서는 행렬을 어디에 사용하는지, 어떻게 하는지 살짝 맛보기 수준으로 제공되서 나쁘지 않았던 것 같다.
추천여부
해당 강의는 무료로 제공되고 있는 지금 듣는게 가장 좋을 것 같다!
유료로 전환된 이후의 금액이 어떻게 될지 모르겠으나, 실습이 더 보강되면서 유료로 전환이 되는거면 정말 추천!
그게 아니라면, 무료일때 미리 듣는 것을 추천한다!
'기타' 카테고리의 다른 글
| [통계 기초] 데이터 분석 공부를 위한 통계지식을 위한 개별 스터디 - 2편 (2) | 2024.03.22 |
|---|---|
| [통계 기초] 데이터 분석 공부를 위한 통계지식을 위한 개별 스터디 - 1편 (0) | 2024.03.21 |
| 캐글 노트북 한글로 번역하는 방법 (크롬 확장팩 사용하기!) (1) | 2024.01.12 |
| 2024년 취업 준비 및 독학 계획 (2) | 2024.01.04 |
| 과정 수료 후 처음 작성하는 글이자 소감? (README) (1) | 2023.12.12 |


